 The multiplicative group modulo p
The multiplicative group modulo p
This page looks at the multiplicative group modulo p for a prime $p$, $\mathbb{Z}_p^*$, which is used in public key cryptography using discrete logarithms. We consider some of the properties relevant to its use in cryptography and recap on some basic group theory. We assume you understand modular arithmetic and congruences and some basic group theory (definition, axioms, subgroups).
Recommended reading
- A Concrete Introduction to Higher Algebra by Lindsay N. Childs.
- Topics in Group Theory by Geoff Smith and Olga Tabachnikova.
- Cryptography Theory and Practice by Douglas R. Stinson.
Affiliate disclosure: we get a small commission for purchases made through the above links
The multiplicative group modulo p is the set of $p-1$ elements $\{1,2,\ldots,p-1\}$ under the group operation multiplication modulo $p$, where $p$ is a prime.
"multiplicative" = we only care about multiplying the elements
"modulo p" = we do our multiplication operations modulo p
"group" = it has the properties of a group (see below)
Note that there is no zero in the set, that all the elements are pairwise incongruent to each other modulo $p$, and that no element is divisible by or has a common factor with $p$. We'll use these properties later on. See also note 1.
The group is denoted by $\mathbb{Z}_p^*$, but you may also come across $\mathbb{Z}_p^{\times}$, $\mathbb{F}_p^*$, $GF(p)^*$, $(\mathbb{Z}/p\mathbb{Z})^*$ and other similar variants.
It satisfies the five axioms for an Abelian group.
- G1 Closure. Any two elements in the set multiplied together modulo $p$ give another element in the set.
- G2 Identity. The number 1 is the multiplicative identity and gives $1\cdot x = x = x\cdot 1$ for any $x$ in the set.
- G3 Inverses. Every element $x$ in the set has a corresponding inverse element $x^{-1}$ in the set such that $xx^{-1} = 1 = x^{-1}x \pmod{p}$.
- G4 Associativity. For any elements $a,b,c$ in the set, $a(bc)=(ab)c\pmod{p}$.
- G5 Commutativity. For any two elements $a,b$ in the set, $ab=ba\pmod{p}$.
The axioms G4 and G5 are inherited from the multiplicative properties of the integers $\mathbb{Z}$, as is the identity axiom G2. The same rules of associativity and commutativity apply under modular multiplication, so we don't need to worry about the order we write the terms in our expressions and we don't need to use brackets (unless we choose to). The two axioms G1 and G3 require some further explanation.
To show that the closure axiom (G1) holds we need to show that the product of two elements can never be zero. Suppose $xy\equiv 0 \pmod{p}$ for two elements $x,y$ in the set. This implies that either $x$ or $y$ is divisible by $p$, which is not true: a contradiction.
To show that an inverse exists for every element (axiom G3) we observe that no element has a common factor with $p$ or is divisible by it. Thus, for any element $x$ in the set, $\gcd(x,p)=1$. By Bezout's identity that means there are integers $r$ and $s$ such that $xr + ps = 1$. We can rewrite this as $xr = 1 - ps$ or $xr \equiv 1\pmod{p}$. We conclude that $r$ (or $r\mod p$) is the multiplicative inverse of $x$.
A recap on group theory
A group $(G,\ast)$ is a set $G$ of elements (a.k.a. members) under a group operation $\ast$ which together satisfy the first four group axioms G1-G4.
From these four axioms, we can go on to prove that the identity element is unique and that each element has a unique inverse. The identity element is sometimes denoted $e$.
If the group operation is commutative (and so axiom G5 is satisfied), we call $G$ an Abelian group, named after the Norwegian mathematician Niels Abel. An example of a group that is not commutative is the set of $2 \times 2$ matrices under matrix multiplication. Note that the group $\mathbb{Z}_p^*$ is Abelian.
A subgroup $H$ of a group $G$ is a subset of elements $H \subseteq G$ that includes the identity element and obeys the closure and inverses axioms. The associativity and commutativity properties come for free.
The order of a group is the number of elements in the set $G$, denoted $|G|$.
If the set $G$ is finite (i.e. $|G|\lt \infty$) we call the group a finite group. The group $\mathbb{Z}_p^*$ is finite and has order $p-1$.
Exponentiation
For an element $a\in G$ we define $a^n$ (read “$a$ to the power $n$”) as $a^n = a\ast a \ast \cdots \ast a$ [$n$ times].
For the group $\mathbb{Z}_p^*$, the $a^n$ notation corresponds to the usual meaning of modular exponentiation where $a^n$ is the element $a$ multiplied by itself $n$ times (modulo $p$, of course).
$a^ma^n = a^{m+n}$
$\left(a^m\right)^n = a^{mn}$
Note that the indices $m$ and $n$ are integers, not group elements, so you can add and multiply them in the usual way. For example, we can write $\left(a^m\right)^n = a^{mn} = a^{nm} = \left(a^n\right)^m$. They work with negative values, too, if we define $a^{-m} = \left(a^{-1}\right)^m$. For a zero exponent, $a^0=1$, the identity element.
The order of an element
The order of an element $a\in G$ is defined as the smallest integer $m$ such that $a^m = 1$. We denote this as $\ord(a) = m$. (Note this is not the same as the order of the group.)
Cyclic groups and generators
If there exists an element $g\in G$ with order equal to $|G|$ then we say the group is cyclic. We say the element $g$ generates the group and that $g$ is a generator or primitive element of the group.
All cyclic groups are Abelian but not all Abelian groups are cyclic. All subgroups of a cyclic group are also cyclic.
Not all elements of a cyclic group $G$ generate the group. An element $a$ of order $m \lt |G|$ will generate a subgroup of order $m$, since by definition $a^m=1$ and so the elements will start repeating after $a^m$ since $a^{m+1} = a^1$.
We denote the set of elements generated by an element $a$ as $\langle a\rangle$. So if $\ord(a)=m$ then $\langle a\rangle = \{ a^1, a^2, \ldots, a^m \}$.
Lagrange's theorem
Lagrange's theorem is one of the first "interesting" theorems about groups.
Theorem (Lagrange). If $G$ is a finite group and $H$ is a subgroup of $G$, then the order of $H$ divides the order of $G$.
A corollary of this, sometimes given as Lagrange's theorem itself, is
If $G$ is a finite group of order $n$ and $g\in G$, then the order of $g$ divides $n$.
Another corollary is that a group with order $|G|$ equal to a prime number is always cyclic.
Back to $\mathbb{Z}_p^*$
Interestingly, the group $\mathbb{Z}_p^*$ is always cyclic, even though its order $p-1$ is not a prime (well, for $p\gt 3$). Keith Conrad [CONRAD] gives six different proofs of this.
This means that for some $g \in \mathbb{Z}_p^*$ we have
Fermat's Little Theorem
Note, too, that for any element $a\in \mathbb{Z}_p^*$ we always have $a^{p-1} = 1$. This is a consequence of Lagrange's theorem and leads in fact to a very short proof of Fermat's Little Theorem, which can be stated as
Theorem (Fermat). For any prime $p$ and any integer $a$ not a multiple of $p$, $a^{p-1} \equiv 1 \pmod{p}$.
Reducing exponents
In any cyclical group with order $m$ we can reduce exponents modulo $m$, so $a^i\cdot a^j = a^{i+j \pmod{m}}$. This follows from the property $a^m=1$.
Hence in $\mathbb{Z}_p^*$ we can reduce exponents modulo $p-1$, so $a^i\cdot a^j = a^{i+j \pmod{p-1}}$. For example:
This can be confusing since we do multiplication modulo $p$ but reduce the exponents modulo $p-1$. It is, however, a useful simplification trick when doing computations by hand.
Generators with $p=11$
Consider the case where $p=11$, so the group $\mathbb{Z}_{11}^* = \{ 1,2,\ldots,10 \}$ with order $p-1=10$.
Consider the element $g=2$ and the elements generated by it (all computed modulo $p$).
That is, $\langle 2\rangle = \{ 2,4,8,5,10,9,7,3,6,1 \} = \mathbb{Z}_{11}^*$, and $\ord(2)=10$.
But the element $g=3$ only generates a subgroup of order 5.
That is, $\langle 3\rangle = \{ 3,9,5,4,1 \}$, so $\ord(3)=5$.
And the element $g=10$ only generates a subgroup of order 2.
That is, $\langle 10\rangle = \{ 10,1 \}$, so $\ord(10)=2$.
For such a small group, we can compute the order of all the elements directly.
| $a$ | $\langle a\rangle$ | $\ord(a)$ |
|---|---|---|
| 1 | {1} | 1 |
| 2 | { 2,4,8,5,10,9,7,3,6,1 } | 10 |
| 3 | { 3,9,5,4,1 } | 5 |
| 4 | { 4,5,9,3,1 } | 5 |
| 5 | { 5,3,4,9,1 } | 5 |
| 6 | { 6,3,7,9,10,5,8,4,2,1 } | 10 |
| 7 | { 7,5,2,3,10,4,6,9,8,1 } | 10 |
| 8 | { 8,9,6,4,10,3,2,5,7,1 } | 10 |
| 9 | { 9,4,3,5,1 } | 5 |
| 10 | { 10,1 } | 2 |
Note that the order of any element, $\ord(a) \in \{1,2,5,10\}$, divides the order of the group $(10)$.
In fact, for any prime $p$, we have the following:
- The order of $1$ is always 1.
- The order of $p-1$ is always $2$, since $(p-1)^2 = p^2 - 2p + 1 \equiv 1\pmod{p}$.
- There are exactly $\phi(p-1)$ generators of the group, where $\phi(n)$ is Euler's totient function, the number of positive integers less than $n$ that are coprime to $n$.
In our case for $p=11$, $\phi(p-1)=\phi(10)=\phi(2)\phi(5) = (2-1)\cdot (5-1) = 4$, and we see that we indeed have exactly 4 generators of the group, namely $(2,6,7,8)$.
In fact, if $d$ is a divisor of $p-1$ then there are $\phi(d)$ generators of order $d$.
Finding a generator
There are two methods to find a generator for $\mathbb{Z}_p^*$, both impracticable for the large 1000-plus-bit primes we use in cryptography.
The first method is to choose a candidate integer $a \in \mathbb{Z}_p^*$ and show that $a^i\neq 1$ for $i=1,\ldots,p-2$. This becomes a lot of work to do for large prime numbers $p$.
The second method is to factorize $p-1$ and use the property that $a$ is a generator if and only if $a^{(p-1)/q} \not\equiv 1 \pmod{p}$ for all primes $q$ that divide $p-1$. So we only need to test our candidate $a$ against all the prime factors of $p-1$. But factorizing $p-1$ for a large $p$ is also a difficult problem.
Large prime factor
In cryptography techniques that use discrete logarithms in $\mathbb{Z}_p^*$ it is important to use a generator $g$ that does not generate a small subgroup. Ideally we'd like $g$ to generate the entire group but this is difficult to find for a large $p$. Instead, we make sure that $p-1$ has a large prime factor, $q$, and we make sure that $g$ is a generator of this subgroup.
That is, we select a prime $p$ so that $p = jq + 1$ where $j$ is a large even integer sometimes called the cofactor. We then select a generator $g$ that generates this large subgroup of order $q$ modulo $p$. We know there are $\phi(q) = q-1$ such generators so they should be easy to find.
To find a suitable generator we pick a random number $h$ in the range $1\lt h \lt p-1$ and compute $g = h^j\pmod{p}$. If $g\gt 1$ then use $g$. Otherwise, if $g = 1$ then pick another $h$.
Discrete logarithm
The discrete logarithm of an integer $x$ to the base $g$ modulo $p$ is defined as the integer $n$ such that $g^n\pmod{p}$. That is
The Discrete Logarithm Problem (DLP)
The discrete logarithm problem (DLP) for $\mathbb{Z}_p^*$ is
This is currently an intractable problem for large $p$ in the order of $2^{1024}$.
Similarly, if $p-1$ has a large prime factor $q$ and $g$ is a generator of order $q$, then it is difficult to find $n\in [2,q-2]$ given $g$ and $g^n\pmod{p}$. For a prime $p$ of 1024 bits, the prime factor $q$ should be at least 160 bits.
Notes
- Congruence classes and representatives.
Strictly speaking, the elements of the group are congruence classes.
The congruence class modulo $p$ of the integer $r$ is the set of all integers congruent to $r$ modulo $p$, usually denoted
$[r]_p$. So $[r]_p$ is the set of all integers of the form $r + kp$.
If we are being strict we should write
$\mathbb{Z}_p^* = \{ [1]_p, [2]_p, \ldots, [p-1]_p \}$.Any element $x$ of a congruence class modulo $p$ is called a representative of the class, and a congruence class can be labelled by any element in the class. For example, for $p=5$ we could write, if we wished,$\mathbb{Z}_5^* = \{ 1, 2, 3, 4 \}$, or
$\mathbb{Z}_5^* = \{ 6, 7, 8, 9 \}$, or
$\mathbb{Z}_5^* = \{ 11, 17, 23, 29 \}$.
We can even use Klingon numbers,
$\mathbb{Z}_5^* =$ { ,
,
 ,
,
 ,
,
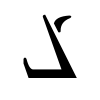 }
The most convenient labelling for $\mathbb{Z}_p^*$ is to use the least positive residues modulo p, $\{ 1,2,\ldots, p-1 \}$. Which brings us back to where we started. There is rarely any advantage in using any other representatives (Klingon mathematicians excepted), so you don't need to worry too much about congruence classes and representatives. The least-positive-residue representation has the bonus that the expression “$a = b \bmod p$” can be used interchangeably with the congruence relation “$a\equiv b\pmod{p}$”. It can, however, be handy in proofs to be able to write the group element $r$ as the integer $r + kp$.
}
The most convenient labelling for $\mathbb{Z}_p^*$ is to use the least positive residues modulo p, $\{ 1,2,\ldots, p-1 \}$. Which brings us back to where we started. There is rarely any advantage in using any other representatives (Klingon mathematicians excepted), so you don't need to worry too much about congruence classes and representatives. The least-positive-residue representation has the bonus that the expression “$a = b \bmod p$” can be used interchangeably with the congruence relation “$a\equiv b\pmod{p}$”. It can, however, be handy in proofs to be able to write the group element $r$ as the integer $r + kp$.
References
- [CHIL09] Childs, Lindsay N. A Concrete Introduction to Higher Algebra, Springer Science+Business Media LLC, 2009.
- [CONRAD] Conrad, Keith. Cyclicity of (Z/(p)), <cyclicFp.pdf>.
- [SMIT00] Smith, Geoff and Olga Tabachnikova. Topics in Group Theory, Springer-Verlag, London, 2000.
- [STIN02] Stinson, Douglas R. Cryptography Theory and Practice, 2nd ed, Chapman & Hall/CRC, 2002.
Acknowledgements
Thanks to Tom Verhoeff for his suggestions on reducing exponents.
Contact us
To comment on this page or to contact us, please send us a message.
This page first published 3 September 2013. Last updated 9 September 2025.

