 Binomial distribution calculator
Binomial distribution calculator
This calculates a table of the binomial distribution for given parameters and displays graphs of the distribution function, f(x), and cumulative distribution function (CDF), denoted F(x). Enter your values of n and p below. There is more on the theory and use of the binomial distribution and some examples further down the page. Click on Calculate table to refresh the table and click on Show graph to see the graphs.
Recommended reading
- Schaum's Easy Outline of Probability and Statistics by John Schiller, A. Srinivasan and Murray Spiegel
- Advanced Engineering Mathematics by Erwin Kreyszig
Affiliate disclosure: we get a small commission for purchases made through the above links
| Binomial | |||
|---|---|---|---|
| f(x) | F(x) | 1 - F(x) | |
| x | Pr[X = x] | Pr[X ≤ x] | Pr[X > x] |
The Binomial Distribution
Suppose we conduct an experiment where the outcome is either "success" or "failure" and where the probability of success is p. For example, if we toss a coin, success could be "heads" with p=0.5; or if we throw a six-sided die, success could be "land as a one" with p=1/6; or success for a machine in an industrial plant could be "still working at end of day" with, say, p=0.6. We call this experiment a trial. Note that the probability of "failure" in a trial is always (1-p).
If the probability of success p in each trial is a fixed value and the result of each trial is independent of any previous trial, then we can use the binomial distribution to compute the probability of observing x successes in n trials.
The binomial distribution is defined completely by its two parameters, n and p. It is a discrete distribution, only defined for the n+1 integer values x between 0 and n.
Important things to check before using the binomial distribution
- There are exactly two mutually exclusive outcomes of a trial: "success" and "failure".
- The probability of success in a single trial is a fixed value, p.
- The result of each trial is independent of any previous trial.
The probability distribution function, f(x)
If a random variable X denotes the number of successes in n trials each with probability of success p, then we say that X ∼ Bin(n, p), and the probability of exactly x successes in n trials Pr[X = x] is given by the distribution function, f(x), computed as follows:
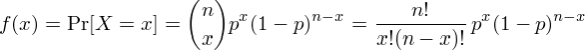
where 0 ≤ x ≤ n.
This is the value in the f(x) column in the table and is the height of the bar in the probability distribution graph. The sum of all these f(x) values over x = 0, 1, …, n is precisely one.
The term
![]() is known as the binomial coefficient,
which is where the binomial distribution gets its name.
This is the number of ways we can choose x unordered combinations from a set of n.
We read this as "n choose x".
It is also written in the form nCx.
is known as the binomial coefficient,
which is where the binomial distribution gets its name.
This is the number of ways we can choose x unordered combinations from a set of n.
We read this as "n choose x".
It is also written in the form nCx.
Terminology and potential for confusion: The function f(x) is sometimes called the probability mass function, in an analogy with the probability density function used for continuous random variables. The corresponding term cumulative probability mass function or something similar is then used for F(x). Other authors use the term probability function for f(x), and reserve the term distribution function for the cumulative F(x). Make your own choice and be consistent.
The cumulative distribution function, F(x)
The cumulative distribution function F(x) = Pr[X ≤ x] is simply the sum of all f(i) values for i = 0, 1, …, x. The value F(n) is always one, by definition.

Example 1
Suppose we toss a fair coin six times, what is the probability of getting
- exactly 4 heads?
- 2 or fewer heads?
The trial in this case is a single toss of the coin; success is "getting a head"; and p=0.5. There are six trials, so n=6. Thus the random variable X ∼ Bin(6, 0.5).
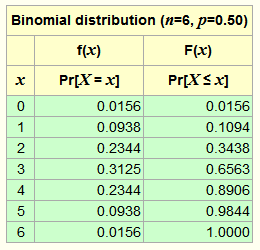
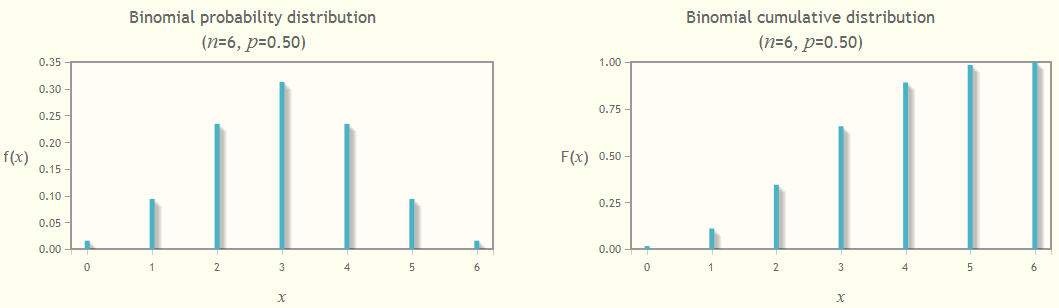
(a) The probability of getting exactly 4 heads out of the six is P[X = 4] = f(4) = 0.2344, the height of the bar at x=4 in the probability distribution graph (the left one).
(b) The probability of getting 2 or fewer heads out of the six is P[X ≤ 2] = F(2) = 0.3438, the cumulative value at x=2 in the right-hand graph (which equals the sum of the bars at x=0, 1 and 2 in the left-hand graph).
Example 2

Suppose we are in a factory with eleven identical machines where our definition of success for one machine is "machine is still working at end of day" with probability p = 0.6 (or, put the other way, there is a 40% chance that a machine will break down during the day). Of the 11 machines, what is the probability that:
- exactly 6 machines are still working at the end of a day?
- at least 6 machines are still working at the end of a day?
Check: In this case, a trial is whether or not a given machine is either working at the end of a day or it isn't. There are exactly two mutually exclusive outcomes. We define success as a "machine is still working at end of day". The probability of success is p = 0.6. This is a fixed value and is independent of any other event. Thus we have satisfied the conditions to use the binomial distribution.
We have 11 machines and so n = 11. Our random variable X is the number of successes in n = 11 trials; that is, X is the number of machines still working at the end of the day. We have X ∼ Bin(11, 0.6).
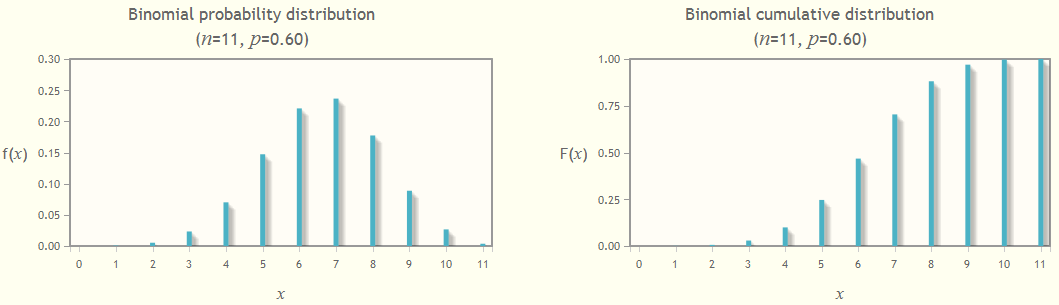
The answer to part (a) is Pr[X = 6], the probability that X is exactly equal to 6. This is the value of f(6)=0.2207, from the middle column of the table, or the height of the bar at x = 6 in the left-hand probability distribution graph. Therefore the probability that exactly 6 machines are still working at the end of a day is 0.2207.
The answer to part (b) is Pr[X ≥ 6], the probability that X is greater than or equal to 6. This is the sum of the bars in the left-hand graph for x = 6 to x = 11. We use the cumulative probability function F(x) = Pr[X ≤ x] to work this out.
Pr[X ≥ 6] = 1 - Pr[X < 6]
= 1 - Pr[X ≤ 5]
= 1 - 0.2465
= 0.7535
Therefore the probability that at least 6 machines are still working at the end of a day is 0.7535.
Other statistical calculators
See our Chi-square calculator which allows you to compute the p-value for a given chi-square statistic, or compute the inverse given the p-value, with the option to display a graph of your results.

An aside on Post-Quantum Cryptography
Are you interested in Post-Quantum Cryptography (PQC)? Then see our pages
- SPHINCS+ (now called SLA-DSA Stateless Hash-Based Digital Signature Standard), a stateless hash-based signature scheme chosen as one of the first quantum-resistant signature algorithms in NIST's post-quantum cryptography standardization project.
- A simple lattice-based encryption scheme, the foundation of the post-quantum cryptosystem ML-KEM Module-Lattice-based Key-Encapsulation Mechanism Standard (formerly CRYSTALS-Kyber), with Python code.
References
- NIST/SEMATECH. e-Handbook of Statistical Methods, http://www.itl.nist.gov/div898/handbook/, Binomial Distribution, (accessed April 2013).
- Kreyszig, Erwin. Advanced Engineering Mathematics, 3rd ed., Wiley, 1972.
- Spiegel, MR, J Schiller, RA Srinivasan, Schaum's Easy Outline of Probability and Statistics, McGraw-Hill, 2001.
Acknowledgements
Thanks to Jim Hussey for pointing out a typo with the ≥ symbol.
Rate this page
Contact us
To comment or provide feedback on this page, please send us a message.
This page first published 25 April 2013 and last updated 9 September 2025.

