 Chi-square calculator
Chi-square calculator
To view the graph of the χ2 distribution for your calculated values, click on the show graph button after doing the calculation.
Compute the p-value for a chi-square distribution
Recommended reading
- Handbook of Mathematical Functions by Milton Abramowitz and Irene Stegun
- Numerical Recipes in C by William H. Press, Flannery,Teukolsky and Vetterling
- Schaum's Easy Outline of Probability and Statistics by John Schiller, A. Srinivasan and Murray Spiegel
Affiliate disclosure: we get a small commission for purchases made through the above links
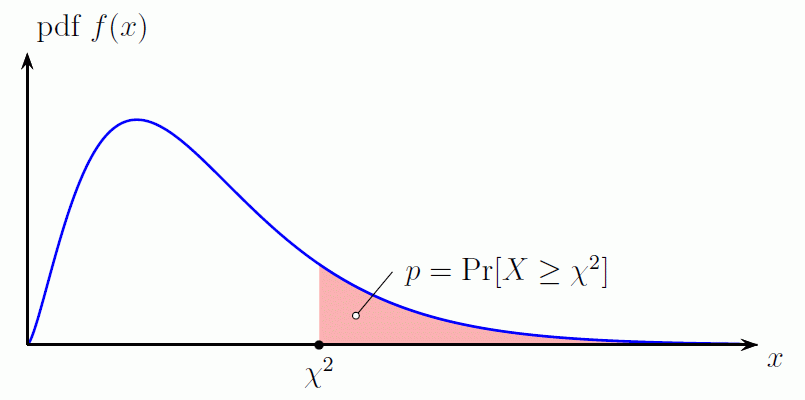
The p-value is the area under the chi-square probability density function (pdf) curve
to the right of the specified χ2 value.
In Excel: p = CHIDIST(χ2,ν).
See Chi-square formulae for more details of the mathematics.
Compute the inverse of the p-value for a chi-square distribution
This is the value of χ2 that will give the specified p-value for the chi-square distribution.
In Excel: χ2 = CHIINV(p,ν).
Table of selected percentiles
See a table of selected percentiles of the chi-square distribution computed using the Javascript calculation engine behind this page. This is the usual table we see in textbooks. You can see a comparison of our results with those given by Excel.
Other statistical calculators
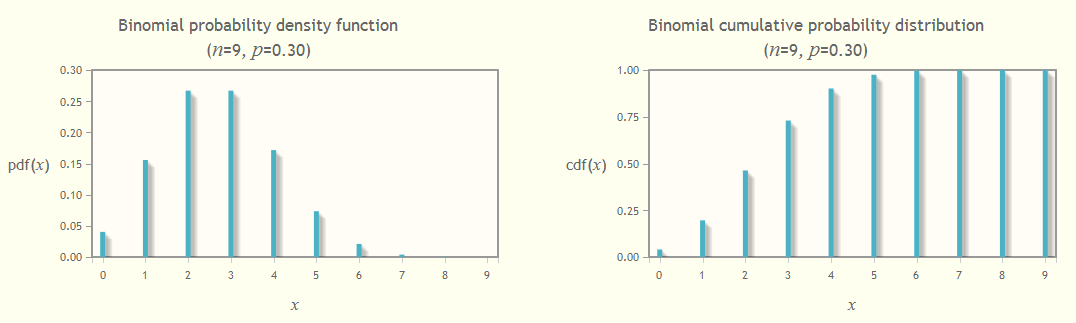
See our Binomial distribution calculator which calculates a table of the binomial distribution for given parameters and displays graphs of the distribution function, f(x), and cumulative distribution function, F(x).
An aside on Post-Quantum Cryptography
Are you interested in Post-Quantum Cryptography (PQC)? Then see our pages
- SPHINCS+ (now called SLA-DSA Stateless Hash-Based Digital Signature Standard), a stateless hash-based signature scheme chosen as one of the first quantum-resistant signature algorithms in NIST's post-quantum cryptography standardization project.
- A simple lattice-based encryption scheme, the foundation of the post-quantum cryptosystem ML-KEM Module-Lattice-based Key-Encapsulation Mechanism Standard (formerly CRYSTALS-Kyber), with Python code.
References
- [1] Abramowitz, M. and IA Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, National Bureau of Standards, Applied Mathematics Series 55, Tenth Printing, 1972.
- [2] Menezes, AJ, PC van Oorschot and SA Vanstone, Handbook of Applied Cryptography, CRC Press LLC, 1997.
- [3] NIST/SEMATECH. e-Handbook of Statistical Methods, http://www.itl.nist.gov/div898/handbook/ (accessed January 2013).
- [4] Press, WH, SA Teukolsky, WT Vetterling and BP Flannery, Numerical Recipes in C: The Art of Scientific Computing, Second Edition, Cambridge University Press, 1992.
- [5] Spiegel, MR, J Schiller, RA Srinivasan, Schaum's Easy Outline of Probability and Statistics, McGraw-Hill, 2001.
Acknowledgements
Many thanks to Phil O'Sullivan, statistician extraordinaire, for his help and advice on this subject.
Rate this page
Contact us
To comment or provide feedback on this page, please send us a message.
This page last updated 9 September 2025.

